Douglas Stebila
Generic GF(2m) arithmetic in software and its application to ECC
Abstract
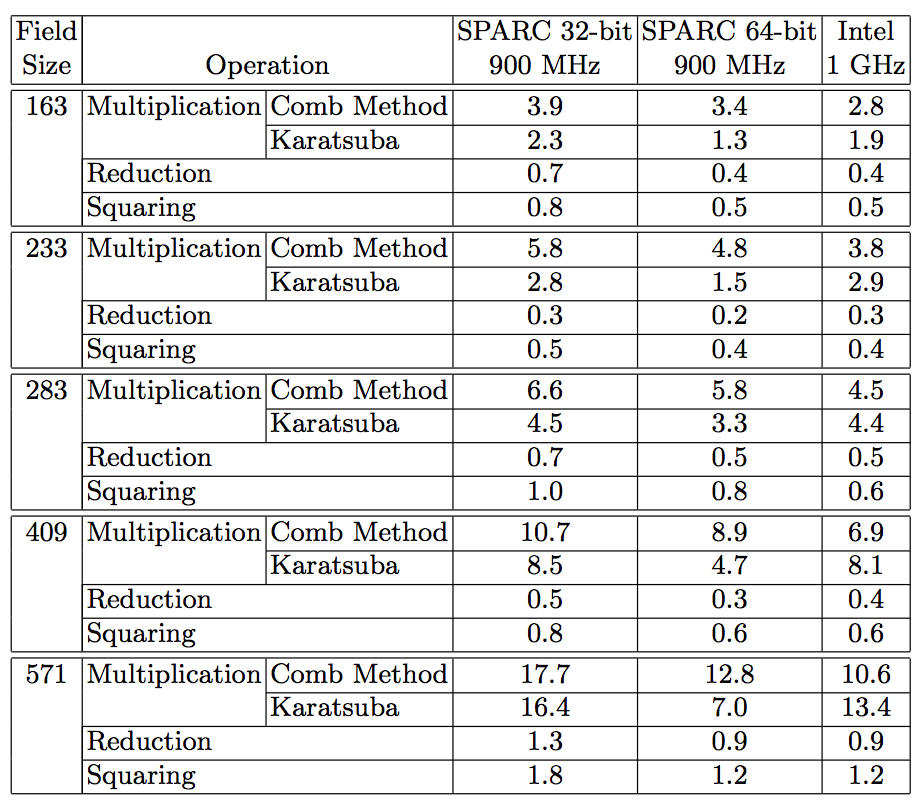
This work discusses generic arithmetic for arbitrary binary fields in the context of elliptic curve cryptography (ECC). ECC is an attractive public-key cryptosystem recently endorsed by the US government for mobile/wireless environments which are limited in terms of their CPU, power, and network connectivity. Its efficiency enables constrained, mobile devices to establish secure end-to-end connections. Hence the server side has to be enabled to perform ECC operations for a vast number of mobile devices that use variable parameters in an efficient way to reduce cost. We present algorithms that are especially suited to high-performance devices like large-scaled server computers. We show how to perform an efficient field multiplication for operands of arbitrary size, and how to achieve efficient field reduction for dense polynomials. We also give running times of our implementation for both general elliptic curves and Koblitz curves on various platforms, and analyze the results. Our new algorithms are the fastest algorithms for arbitrary binary fields in literature.
Keywords: binary fields, dense field polynomials, field multiplication, field reduction, elliptic curves, Koblitz curves
Reference
André Weimerskirch, Douglas Stebila, Sheueling Chang. Generic GF(2m) arithmetic in software and its application to ECC. In Reihaneh Safavi-Naini, Jennifer Seberry, editors, Proc. 8th Australasian Conference on Information Security and Privacy (ACISP) 2003, LNCS, vol. 2727, pp. 79-92. Springer, July 2003. © Springer.